Introducing Integers

Integers: Eli and the Magic Peanuts Model

This model was developed and used in the CSMP (Comprehensive School Mathematics Program) and remains a wonderful introduction to integers for young children. Eli is an elephant who loves peanuts. As he travels through the jungle, he picks up each and every peanut he sees and places them in his bag. The trouble is that some of the peanuts are magic peanuts. They look the same as regular peanuts, so Eli doesn't know if he's picking up a regular or a magic peanut. The problem is that when a regular and a magic peanut get together, they disappear. Eli is always disappointed to find fewer peanuts in his bag when he stops for a snack.

Young students love this model and using Mathwire-developed resources to "poof" the peanuts when a regular and magic peanut get together. Older students also enjoy this magical introduction.

Eli and the Magic Peanuts Model: Acting Out the Story Tell students the story of Eli: Eli loves peanuts. He finds them on the ground as he roams around the jungle. Each time Eli sees a peanut, he picks it up and adds it to his peanut bag. When he's hungry for a snack, he opens up the bag and counts his peanuts. But, there's a problem. There are regular peanuts and magic peanuts in the jungle. They look the same so Eli can't tell whether it's a regular peanut or a magic peanut. But when a regular peanut and a magic peanut get together in Eli's peanut bag, POOF! they both disappear. So, sometimes when Eli goes to snack, he finds that some of the peanuts have disappeared. Distribute demo-size peanuts (3) and magic peanuts (2) to students and ask them to stand in the front of the room. Ask students to count the total number of peanuts and record this on the board. Tell students: The regular peanuts and the magic peanuts look the same to Eli, but we're going to put magic hats on the magic peanuts so that we can tell the difference.

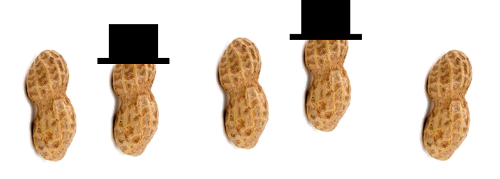
Tell students: We are going to pretend that these are the peanuts that Eli picked up. How many peanuts did Eli pick up? [Student answers 5.] Now, remember that the regular peanuts and the magic peanuts look the same to Eli, but we put a hat on the magic peanuts so we can tell the difference. Will there be 5 peanuts in Eli's bag when he decides to have a snack? [Call on students and ask them to explain why or why not.] Help students rearrange themselves so that a regular peanut and a magic peanut are paired.

For great ceremony, you might use a magic wand to Poof! a regular peanut and a magic peanut and have them disappear. [Students simply move to the side together.] Continue Poofing pairs of a regular peanut and a magic peanut, until there are no pairs left. Now ask the students how many peanuts are left in Eli's bag and whether it's a regular peanut or a magic peanut? [Accept answers.]

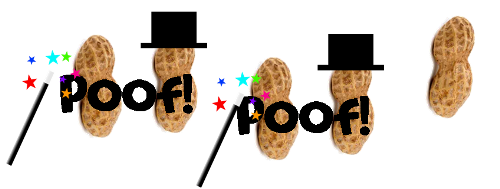
So, even though Eli picked up 5 peanuts, two of them were magic peanuts and they made some of the regular peanuts disapper. The answer to the problem is that Eli found only one peanut in his bag when he decided to eat a snack. Poor Eli!!!

	Eli and the Magic Peanuts Model: Using 2-color Counters & Eli Mat Students use the Eli mat and 2-color counters. They place red counters in the Magic Peanuts space on the mat. They place yellow (or white) counters in the Regular Peanut space on the mat. NOTE: Copy the Eli mat onto card stock for durable classroom use and/or place the mat in a clear sheet protector for student use. 2-color counters are widely available in either red-white or red-yellow color combinations. If these are not available, use two different color tiles or chips so that students easily recognize the regular and magic peanuts.

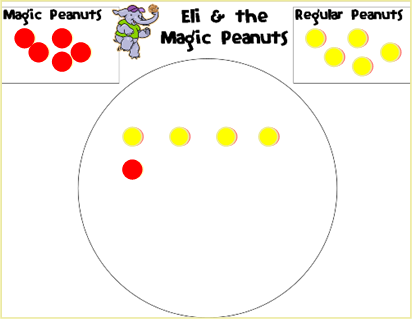
	Modeling the Problem on the Mat PROBLEM: Eli picked up 4 regular peanuts and 1 magic peanut. How many peanuts were left in his bag when he decided to have a snack? Students move 4 yellow counters (regular peanuts) and 1 red counter (magic peanut) to the circle (Eli's peanut bag). Students make any pairs that they can and move these close together.

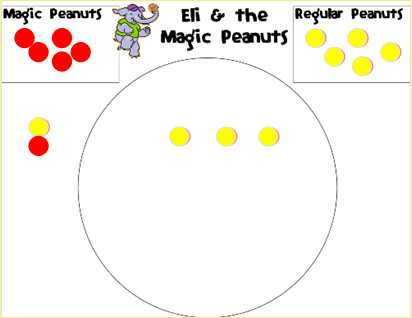
	POOF! Students POOF! peanuts by moving pairs (1 red and 1 yellow) outside the circle. Then, students count how many peanuts are left in the bag for Eli to eat. The answer to this problem is that there were 3 peanuts left in the bag when Eli decided to eat a snack. Dowload the Eli & the Magic Peanuts worksheet. NOTE: students should use the Eli mat and 2-color counters to solve the problem, then use markers to draw and color the solution on the worksheet.

Homemade Eli Manipulatives
Paper Bag Demo-Size Peanuts	Craft Foam Demo-Size Peanuts	Student Foam Peanuts

Eli and the Magic Peanuts Model: CSMP Project

Eli's Magic Peanuts was introduced in the Comprehensive School Mathematics Project curriculum at the first grade level. Mathwire has used this model because it is such an effective introduction to integers for young learners. Hoever, in our experience, older students and adults enjoy the model as well.

View the Eli introduction in the first grade curriculum. NOTE: You will have to scroll through the document to Lesson F114, page 4-473 for a multi-page presentation. Here you'll find the original representations and story.