Investigating Growing Patterns

Featured Topic: Investigating Growing Patterns

Introduce elementary students to the concept of functions by investigating growing patterns. Visual patterns formed with manipulatives are especially effective for elementary students and allow them to concretely build understanding as they first reproduce, then extend the pattern to the next couple of stages.

Following this concrete modeling, the teacher introduces the use of an input-output table to organize data about the number of blocks used for each stage of the pattern. The table helps quantify the pattern so that students see both the growing pictures and the growing numbers in the table. They can note the change from stage to stage and work to explain how the change in the table matches the change in the picture of the growing pattern.

Finally, students can learn to write a general rule that will work for any stage of the pattern without having to build it or know how many blocks were used in the stage before it. This is an important abstraction of the pattern and the rule must make sense to students and be in their own words or in their own mathematical notation that reflects the level of their current understanding.

Fir Tree uses pattern block triangles to create growing fir trees. Students must extend the pattern, complete the table of values and describe the 10th tree.
Hexagon Dragons requires students to extend the pattern, create an input/output table to describe the growing pattern, then draw and/or describe the 10th dragon in words. An extra challenge asks students to generate a rule for this pattern so that Miguel can figure out how many blocks he will need to build a dragon of any size.
Tables & Chairs Investigation challenges students to find a rule to describe the relationship between the number of small square restaurant tables placed together in a line and the number of diners that can be seated at the larger table if only one person sits on each side.
Caterpillar Problem from Marilyn Burns, Math Solutions, asks students to build, extend and create a table of values for the growing caterpillar.
Rocket Problem from Marilyn Burns, Math Solutions, asks students to build, extend and create a table of values for the growing rocket.

CHALLENGE: Student-Created Growing Patterns

Students enjoy this pictorial introduction to growing patterns. Once students begin to notice and describe the patterns found in several classic math patterns, they become more sophisticated in their own pattern-making. Teachers find that students naturally start arranging manipulatives to form other animals, characters, etc. Capitalize on this natural inclination to "mess around" by challenging students to create their own growing patterns and design an activity their classmates can do in the math pattern center.

Samples of growing pattern problems created by fourth graders:

Check back for pictures and samples of student work coming soon.

Function Scrapbook

In case you need some ideas to get started, the following are samples of growing pattern problems created by ED 556 students at Monmouth University in West Long Branch, NJ during the Fall 2004 session. In each case, students should draw and/or describe the next couple of stages in the pattern and create an input/output table to describe the relationship between the stage and the number of blocks used. Students should be challenged to write a rule in words and more capable students should be challenged to write a general mathematical rule that would calculate the number of blocks needed for any given stage.

Apple Trees, created by Kirsten Hofmann
Boats, created by Jennifer Oberc
Butterflies, created by Jennifer Oberc
Cat Whiskers, created by Lorraine McEvoy
Dinosaur Spikes, created by Jennifer Farber
Dogs on the Block, created by Lorraine McEvoy
Fish, created by Kirsten Hofmann
Flowers, created by Heather Payne
Ice Cream Cones, created by Deanna Sanford
Kites and Tails, created by Cynthia Gomez
Ladybugs, created by Jennifer Oberc
Patty the Plant, created by Cara Lynn Scott
Rockets, created by Kirk Pelletier
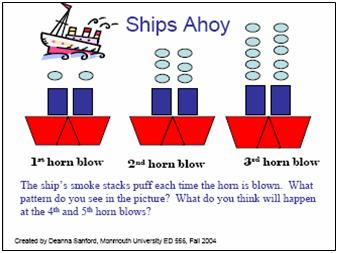
Ships Ahoy, created by Deanna Sanford
Swans, created by Beth Watts
Trains, created by Kathleen Rooney
Turtles, created by Kirsten Hofmann

Featured Technology Links: Function Machines

These sites provide students with additional online practice with function machines. Teachers may differentiate practice for students by structuring the use of practice sites to best meet the developing needs of students in the class.

Function Machine for Grades 3-4
Function Machine for Grades 5-6
Building with Functions for Grades 5-8
Project Interactivate's Whole Number Cruncher uses only addition and multiplication rules to eliminate negative number outputs
Project Interactivate's Number Cruncher
NLVM Virtual Manipulative: Function Machine allows students to drag numbers into the function machine and see the output. Students are then challenged to extend the rule to additional input numbers by typing in the correct output for these numbers.

Literature Connections

These books provide literature connections that lend themselves to the introduction of functions as growing patterns. First, investigate and quantify the patterns in the books using T-charts or input/output tables to record the data. Next, search for patterns and identify rules. Finally, extend this experience to similar patterns to give students more practice in using these mathematical tools.

Two of Everything by Lily Toy Hong recounts a Chinese folk tale. The farmer finds a magic pot which doubles everything that is put into it. This humorous story is a great introduction to function machines and input/output tables as teachers make the transition to the "doubling pot" and recording information in an input/output table. Next, teachers change the rule for the magic pot and keep it secret. Students supply input numbers and the teacher records the output numbers for each. Students try to guess the magic pot's current rule. This could then be extended to a growing pattern by simply using the last output as the next input, applying the rule and repeating the process.

Download the Magic Pot Workmat for students to use in sheet protectors.

See 5 Coins and the Magic Doubling Pot or 1000 Coins for another take on this growing pattern problem that challenges students to figure out which is the best deal.

One Grain of Rice: A Mathematical Folktale, illustrated by Demi, introduces the power of doubling as the main character outsmarts others by asking for just one grain of rice the first day. Each successive day she will get double the amount of the day before. Students are always amazed at how quickly this pattern grows.

See detailed lesson plan for Find a Pattern with "One Grain of Rice" which includes PDF handouts.

The Most Popular Food in the World: Rice challenges students to go beyond the obvious in this folktale and figure out how many people the rice would feed, etc., weaving measurement and real-life applications into extensions of this folktale. Several different level challenges are available on the site to best meet the needs of different students in middle school math classes.

See The Million $ Mission for a modern day job offer investigation which challenges students to identify the best payment plan.

The King's Chessboard, by David Birch, also introduces the power of doubling as the wise man outsmarts the king by asking for just one grain of rice on the first square of the chessboard. For each successive square he will get double the amount of the previous square. Although this request initially sounds meager, the king soon discovers that he has been outsmarted as he tries to supply the rice for each of the 64 squares of the chessboard.

See the King's Chessboard Solution.

Instructional Resources

There are many professional books that treat the concept of growing patterns and its relationship to the developing concept of functions for elementary students. The abstract concepts of the high school course on functions are developed from kindergarten through the elementary grades by using manipulatives and real-life situations that lend themselves to pictures, organizing data in a table and trying to write a rule in words and/or mathematical symbols to describe the growing pattern.

Math Solution's Lessons for Algebraic Thinking series from Marilyn Burns is available for different grade bands: K-2, 3-5 and 6-8. This series builds on drawing growing patterns and recording the number of pieces used in input/output tables to discover a pattern or rule. This series discusses how to present the problem, teacher questioning and student discussion and includes samples of student work.
NCTM's Navigating Through Algebra series is available for different grade bands: preK-2, 3-5 and 6-8. This series offers classroom activities that meet the objectives of the NCTM Standards on Patterns & Algebra.
Algebra Thinking: First Experiences is a binder of activities that develop algebraic thinking including many growing pattern problems. This is a terrific, classroom-ready collection of handouts that can be copied for students or made into an overhead to stimulate algebraic thinking and discussion. This early collection was designed for Grades 5-8, but 3rd and 4th grade students could easily tackle many of the growing patterns problems.
Beginning Algebra Thinking by Shirley Hoogeboom & Judy Goodnow is available for Grades 3-4 or Grades 5-6. Each book presents a series of pictorial lessons to help students develop the connection between pictures/manipulatives and the input/output table and rule. All activities are masters that can be copied for students or used as an overhead with students working in journals to reproduce, extend and solve the pattern problems.

Additional Growing Pattern Resources on the Internet

See Growing Patterns, Lesson 8 in the NCTM Illuminations Powerful Patterns series.
Growing Patterns offers classroom activities designed to introduce K-2 students to this powerful concept.
Grow a Pattern offers lesson plans, task cards and growing pattern starters to help students investigate growing patterns.
Check out Growing Patterns: Assessment Tasks for some suggested assessment ideas and student work samples for younger students.
Patterns That Grow builds on the pattern found in One Grain of Rice by asking students to figure out how much money they would earn walking the neighbor's dog if there pay starts at a penny and doubles each day.
Consult Patterns & Functions, Grades 6-8. Chapter 5, pages 23-26, presents Growing Patterns as students analyze a growing cat. Chapter 6, pages 27-33, investigates toothpick patterns.
Repeating Patterns presents the growing patterns for a tree and a fish.
About Patterns and Algebra offers concrete activities that help students make the connection between growing patterns formed with manipulatives and input/output tables.